Tabby’s star or KIC 8462852 is dimming once again. At first, it was thought that it was due to an orbiting planet or cloud, but now it is dimming a staggering 3 percent of its luminosity.
Although there are many hypotheses, the most interesting would be the existence of a Dyson swarm, a megastructure possibly employed by aliens to collect energy from celestial bodies. The issue is that so far, scientists have not been able to establish an explanation for the start’s periodic dimming episodes.
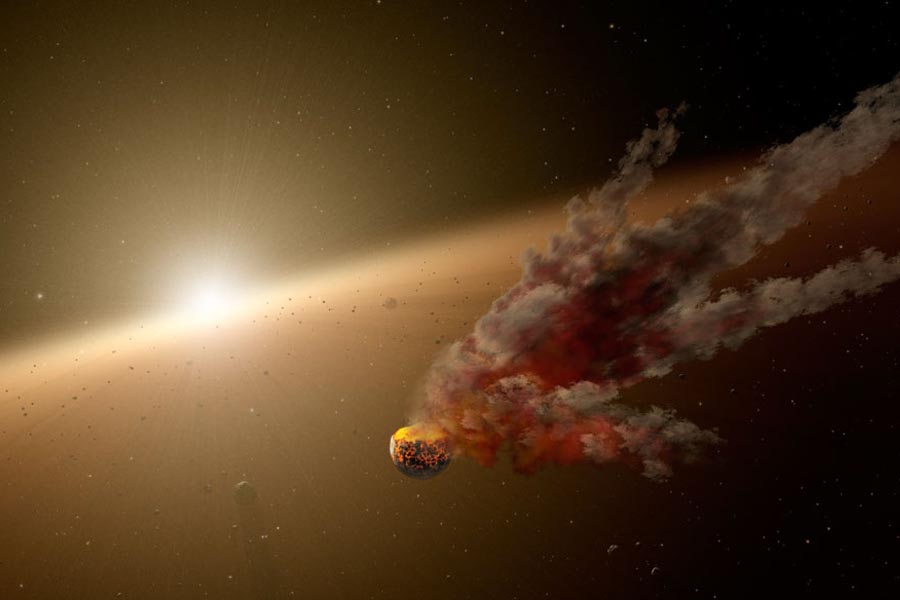
Tabby’s star remains a mystery for everyone
The announcement was made by Jason Wright from Pennsylvania State University on Thursday, who’s conducting a study on the star. He confirmed that the fact that Tabby’s star dims in variable time intervals is in no way a mistake by observers, as the event was witnessed from more than one observatory.
The first observations occurred in 2015, seen through NASA’s Kepler Space Telescope. The technique is often used to find new planets, as sudden dips in a star’s luminosity usually mean that an unregistered object is orbiting it.
In the case of Tabby’s star, the change in magnitude just does not reflect the characteristics of a planet moving in an orbiting fashion.
Other theories include that the star is being orbited by a cloud of comets and gas, although there is no evidence to support the claim.
The plan is to use an object spectra, which allows astronomers to know the type of chemicals that move through a particular region in space. In essence, the object is supposed to “leave a spectral fingerprint,” which will, in turn, emit more of a particular type of light depending on the object’s composition.
The exciting part is that astronomers do not know when the next event will occur, nor if it will ever occur again. Luckily, Tabby’s star is bright enough to be observed by many facilities at the same time, and both novice and professional stargazers are looking upon Boyajian’s discovery.
What everybody hopes is that the dimming is caused by a Dyson swarm, a theoretical solution to the energy needs of advanced civilizations. The precept is that the energy of stars should be harnessed in some way, and the most efficient would be using a Dyson swarm or sphere, which encircles a star and captures its power output. The term was popularized by Freeman Dyson in 1960 after researching credible artificial sources of infrared radiation.
Building such a structure is theoretically possible, although humanity is not able to do so with its current engineering power. The first steps to creating the Dyson swarm would be to employ massive fleets of spacecraft and remote-controlled operators to construct the megastructure around the star carefully. Another impediment would be how the structure should orbit around the star, as predicting such behavior could be easily considered impossible if not ostensibly difficult.
Additionally, a Dyson sphere refers to a spherical shape precisely, while a Dyson swarm refers to the intermediate forms between a sphere and a ring, the latter being the most simplistic approach.
Source: Space

Just use the Hubble space telescope to find it out. I will just hope and desire that this time there will be no secret government agency to come in between such a discovery and hide the real facts about the Dyson structure and the civilization that built it.
I have thought about industry in space for a long time. Designed a few power satellites. The thing which may prove more of a limit in space than energy is heat sinks to get rid of large amount of waste heat. If Tabby’s star is being blocked by artificial object, one possibility is low temperature heat radiators. They would have been seen already if they were running much hotter than 60 deg K. From how slowly they block the light, they seem to be out from the star at Jupiter to Saturn distances. The low temperature is ideal for computers. One question we might ask is why would we build this sort of megastructure?
Dyson Swarm or a partially complete Sphere or other Structure.